Hier zwei Aufgaben aus dem Buch von Johannes Lehmann, eine leichte und eine schwere.
"Gegeben sei ein Haufen. Sein Viertel und sein Ganzes ergeben 15." Wie groß ist der Haufen?
Die Ägypter rechneten hier mit der Methode des falschen Ansatzes. Der funktioniert so: die Größe des Haufens wird erstmal mit einer "günstigen" Zahl angenommen, hier bietet sich 4 an. Davon ein Viertel und ein Ganzes sind 5. Da die gesuchte Zahl aber 15 ist, also 3 mal größer, muß auch der Haufen dreimal größer sein, also 12.
Und jetzt Du: die Hälfe, das Viertel und das Ganze selbst ergeben 10.
Diese Aufgabe stammt von der Wand einer Tempelruine. Sie lautet ungefähr:
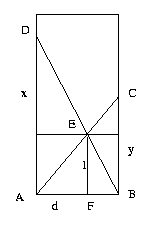
In einen Brunnen (Rechteck in der Abbildung unten) wurden zwei Schilfstengel
(Strecken AC und BD) so gestellt, wie in der Abbildung ersichtlich. Der eine
(AC) ist 3 Maß, der andere 2 Maß lang. Sie berühren sich im Punkt E, der 1 Maß
über dem Grund des Brunnens ist (EF ist das Lot von E auf AB). Wie groß ist d,
der Durchmesser des Brunnens?

<< ![[Interner Link]](intlnk.png) Mathematik im alten Ägypten - Sonstige Erkenntnisse |
Mathematik im alten Ägypten - Sonstige Erkenntnisse |
![[Interner Link]](intlnk.png) Inhalt
Inhalt